Solving the Shortest Path Problem (5) – Benchmarks

This article of 2012 at http://stegua.github.io/ shows, that the type of the priority queue of a shortest path solver is crucial for the solving time.
You have to agree with that, but there is another point to mention: the choice of the graph representation.
I wanted to spend some more time on the comparison of the graph libraries LEMON and BGL and so I modified some of the code and ran the following tests on it.

The code was compiled using GCC 4.8.4 with the the following switches: -O2 -m64 -std=c++11. My test machine is a laptop with an Intel 4-Core i3@2,4 Ghz. You can download the graph instances from the DIMACS site.

BGL’s Dijkstra d-ary Heap (d=4)
Boost’s Graph Library offers two variants of a Dijkstra shortest path solver implementation. A regular one dijkstra_shortest_path and a variant that does not use an internal color map of nodes (dijkstra_shortest_path_no_color_map). Both of them use by default a d-ary Heap with d=4 which is actually a quad heap queue. Unfortunately there is no easy way to change the heap in the dijkstra implementation.

There is no significant difference comparing the solving time of each of them, if you do not change the graph structure.
Using the BGL with street networks you have two flavours of a graph: the widely known adjacency_list and a representation that you should look at if you’re dealing with sparse graphs as street networks are: the compressed_sparse_row_graph.

Here are the results.

[table]
Graph,Nodes,Arcs,m/n ratio, adjacency list [sec],adj RAM footprint [MB],compr. sparse graph [sec], csr RAM footprint [MB]
Western USA,6’262’104,15’248’146,2.4,2.089,606,1.536,458
Central USA,14’081’816,34’292’496,2.4,5.809,1’368,4.477,1’040
USA,23’947’347,58’333’344,2.4,8.664,2’318,6.698,1’770
[/table]
For these graphs the compressed sparse row graph always outperforms the shortest path search on a graph represented with an adjacency_list. The memory usage is also better on compressed sparse row graphs than using adjacency_lists.

LEMON’s Dijkstra d-ary-Heap (d=4)

LEMON’s default Heap for the dijkstra shortest path solver is by default a binary heap. In order to compare against the BGL’s d-ary implementation with d=4 I changed the heap also to a quad heap in LEMON. Now LEMON has three graph structures to offer: ListGraph, SmartGraph and StaticGraph. All types also have the directed variant (e.g. ListDigraph). From ListGraph over SmartGraph to StaticGraph the flexibility of the graph structure will be getting lesser in exchange for efficiency in graph searches. So there is a trade off between flexibility and speed.

Overall LEMON performs better when you look at the solving times as BGL and the StaticGraph of LEMON provides the fastest results.

[table]
Graph,Nodes,Arcs,m/n ratio,ListDigraph [sec],SmartDigraph [sec],StaticDigraph [sec]
Western USA,6’262’104,15’248’146,2.4,1.144,0.985,0.859
Central USA,14’081’816,34’292’496,2.4,2.116,1.887,1.749
USA,23’947’347,58’333’344,2.4,6.358,5.605,5.019
[/table]

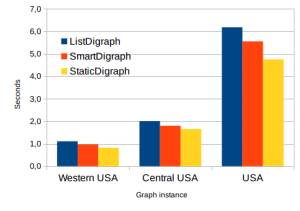
LEMON’s Dijkstra 2-Heap

If you change the Quad Heap priority queue to a Binary Heap in LEMON you gain even more performance. Note that LEMON’s Dijkstra implementation defaults to the Binary Heap, so there would be no need to change the heap in most cases.
[table]
Graph,Nodes,Arcs,m/n ratio,ListDigraph [sec],SmartDigraph [sec],StaticDigraph [sec]
Western USA,6’262’104,15’248’146,2.4,1.109,0.970,0.822
Central USA,14’081’816,34’292’496,2.4,2.005,1.797,1.658
USA,23’947’347,58’333’344,2.4,6.181,5.553,4.750
[/table]

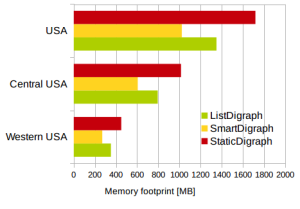
LEMON’s Dijkstra 2-Heap – Memory usage

Now let’s look at the memory usage of LEMON’s 2-Heap Dijkstra using different graph structures.

[table]
Graph,Nodes,Arcs,m/n ratio,ListDigraph [MB],SmartDigraph [MB],StaticDigraph [MB]
Western USA,6’262’104,15’248’146,2.4,352,270,450
Central USA,14’081’816,34’292’496,2.4,795,606,1’016
USA,23’947’347,58’333’344,2.4,1’352,1’024,1’721
[/table]

For me very surprisingly: SmartGraph is the winner! I thought that the static variant is also memory friendlier than the SmartGraph implementation.

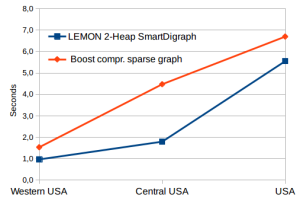
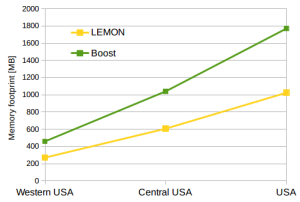
Best bet of BGL’s Dijkstra and LEMON’s Dijkstra

Now if we put all of the results together, I would say LEMON is the clear winner regarding solving time and memory footprint if you go for the default binary heap and the SmartDigraph of LEMON. There is a noteable difference from BGL’s 2,08 secs with an adjacency_list and LEMON’s SmartDigraph with 0,97 secs or even 0,82 secs using the StaticDigraph on the smallest graph. If you use BGL’s dijkstra on street networks you should use the compressed sparse row graph structure.
[table]
Graph,Nodes,Arcs,m/n ratio,LEMON 2-Heap SmartDigraph [sec],LEMON’s RAM fp [MB], Boost compr. sparse graph [sec],Boost’s RAM fp [MB]
Western USA,6’262’104,15’248’146,2.4,0.970,270,1.536,458
Central USA,14’081’816,34’292’496,2.4,1.797,606,4.477,1’040
USA,23’947’347,58’333’344,2.4,5.553,1’024,6.698,1’770
[/table]

[table]
,
[/table]

I forked the repository of stegua and made a few changes to his version of the dijkstra implementations. The code is available on GitHub.